The SLAMICP library performs Iterative Closest Point matching focused on mobile robot self-localization and map creation based on LIDAR data.

The Iterative Closest Point (ICP) is a matching technique used to determine the transformation matrix that minimizes the distance between point clouds.

Example calls to the SLAMICP library using a MATLAB wrapper ( includded in the library as a precompiled MEX file for Windows®):

>> [ P_i, niter, md, O_indx, O_coords, tT_i, M_i, N_i ] = SLAMICP( M_i-1, T_i, inlier_threshold, method, maxiter, P_i-1, N_i-1, Outlier_threshold );

>> [ P_i ] = SLAMICP( M, T_i, inlier_threshold, method, maxiter, P_i-1, N, Outlier_threshold );

The parameters used in the calls are:

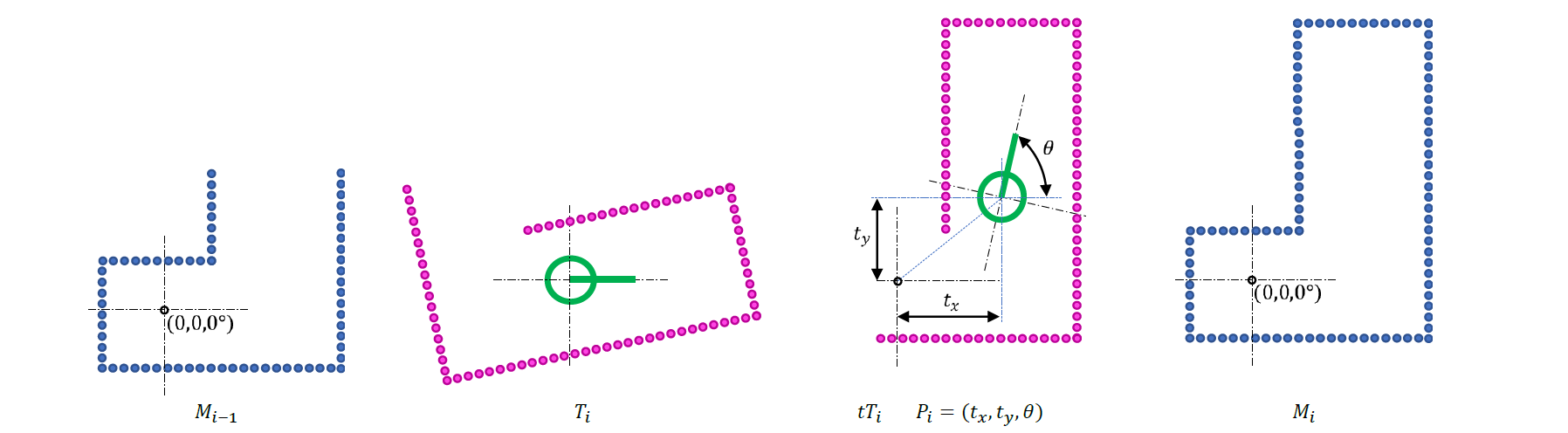
M, is the point cloud defining the map of the environment.

T_i, is the point cloud defining the i'th LIDAR scan that will be matched with the map M.

M_i, is the map updated with the information included in the scan T_i

M_i-1, is the map before incorporating the new information included in the scan T_i

inlier_threshold, is the threshold distance applied to the matched points to classify a point as an inlier (used by the ICP matching), default = 0.3 units

method, the valid ICP methods are: 'point_to_point' or 'point_to_plane' (faster if the normals N are provided)

maxiter, is the maximum number of iterations allowed during the ICP matching

P, is the current position and orientation of the mobile robot in the map M expressed as: P = ( x, y, θ )

P_i, is the current position of the mobile robot in the map M expressed as: P_i = ( x_i, y_i, θ_i )

P_i-1, is the initial guess of P_i, it describes the previous position and orientation of the mobile robot updated with the information of the encoders (if available)

N, are the normals of the map M (use N = [] if the normals are unknown or not used)

N_i, are the normals of the map M_i

N_i-1, are the normals of the map M_i-1 (use N_i-1 = [] if the normals are unknown or not used)

Outlier_threshold, is the threshold distance applied to the matched points to classify a point of tT_i as an outlier (does not affect the ICP matching), default = 0.3 units

niter, is the number of iterations performed during ICP matching

md, is the mean inlier distance (computed from the distance between the matched (inlier) points)

O_index, are the index of the points of T_i classified as outliers

O_coords, are the coordinates of the outliers expressed in the coordinates of M (transformed outliers)

tT_i, is the current (i'th) LIDAR scan (T_i) expressed in the coordinates of M (transformed LIDAR scan)

Representation of example input ( M_i-1, T_i ) and output ( tT_i, M_i ) 2D point clouds:


The SLAMICP library is based on the LIBICP (LIBrary for Iterative Closest Point fitting) which is a cross-platfrom C++ library with MATLAB wrappers for fitting 2d or 3d point clouds with respect to each other. Currently it implements the SVD-based point-to-point algorithm as well as the linearized point-to-plane algorithm. It also supports outlier rejection and is accelerated by the use of k-d trees as well as a coarse matching stage using only a subset of all points.
Compared with the LIBICP, the SLAMICP returns the number of iterations, the mean inlier distance, the outliers, the transformed point cloud and the updated map.

The original LIBICP is avialable in: https://www.cvlibs.net/software/libicp/

When compiled, the MATLAB wrapper of the LIBICP library can be called using:

>> [ Tr_fit ] = icpMEX( M, T_i, Tr_{initial_guess}, inlier_threshold, method );

Where Tr = ( R( θ ), t ) is the transformation matrix that must be applied to T to match M.

The SLAMICP function computes the transformation (P_i) that aligns the input point cloud (T_i) with a reference point cloud (M).
This version is faster when using the method 'point_to_plane' when the normals (N) are precomputed.
A MATLAB wrapper is provided as precompiled MEX file for Windows®.

% Precomputation of the normals N of a (already built) map M
>> N = SLAMICP(M);

% Call to match T_i with M_i-1 and update the map M_i and the normals N_i, faster, ideal for Simultaneous Localization And Mapping (SLAM)
>> [ P_i, niter, md, O_indx, O_coords, tT_i, M_i, N_i ] = SLAMICP( M_i-1, T_i, inlier_threshold, method, maxiter, P_i-1, N_i-1, Outlier_threshold );

% Call to match T_i with M_i-1 and update the map M_i (slowest, the normals are computed on each call)
>> [ P_i, niter, md, O_indx, O_coords, tT_i, M_i ] = SLAMICP( M_i-1, T_i, inlier_threshold, method, maxiter, P_i-1, [], Outlier_threshold );

% Call to match T_i with M without updating the map (faster), ideal for self-localization
>> [ P_i, niter, md, O_indx, O_coords, tT_i ] = SLAMICP( M, T_i, inlier_threshold, method, maxiter, P_i-1, N, Outlier_threshold );

% Call to match T_i with M without updating the map (slower, the normals are computed on each call)
>> [ P_i, niter, md, O_indx, O_coords, tT_i ] = SLAMICP( M, T_i, inlier_threshold, method, maxiter, P_i-1, [], Outlier_threshold );

>> [ P_i, niter, md, O_indx, O_coords ] = SLAMICP( M, T_i, inlier_threshold, method, maxiter, P_i-1, N, Outlier_threshold );   % faster
>> [ P_i, niter, md, O_indx, O_coords ] = SLAMICP( M, T_i, inlier_threshold, method, maxiter, P_i-1, [], Outlier_threshold );

>> [ P_i, niter, md ] = SLAMICP( M, T_i, inlier_threshold, method, maxiter, P_i-1, N, Outlier_threshold );   % faster
>> [ P_i, niter, md ] = SLAMICP( M, T_i, inlier_threshold, method, maxiter, P_i-1, [], Outlier_threshold );

>> [ P_i, niter] = SLAMICP( M, T_i, inlier_threshold, method, maxiter, P_i-1, N);   % faster
>> [ P_i, niter] = SLAMICP( M, T_i, inlier_threshold, method, maxiter, P_i-1, []);

>> P_i = SLAMICP( M, T_i, inlier_threshold, method, maxiter, P_i-1, N);      % fastest, ideal for mobile robot self-localization, P_i = ( x_i, y_i, θ_i )
>> P_i = SLAMICP( M, T_i, inlier_threshold, method, maxiter, P_i-1, []);      % performing mobile robot self-localization, P_i = ( x_i, y_i, θ_i )

% Display the help and usage instructions
>> SLAMICP( );

% Obtain the outliers of tT_i (transformed T_i according to P_i ), matching and merging only the outliers of tT_i (listed in O_coords ) with M_i-1 (no ICP iterations) to create M_i
>> [ ~, ~, ~, O_index, O_coords, tT_i, M_i ] = SLAMICP( M_i-1, T_i, inlier_threshold, method, 0, P_i, Outlier_threshold );

% Obtain the outliers of tT_i (transformed T_i according to P_i )
>> [ ~, ~, ~, O_index, O_coords, tT_i] = SLAMICP( M, T_i, inlier_threshold, method, 0, P_i, Outlier_threshold );

% Obtain tT_i (transformed T_i according to P_i ) and merge all points of tT_i (all are outliers because Outlier_threshold = 0 ) with M_i-1 (no ICP iterations) to create M_i
>> [ ~, ~, ~, O_index, O_coords, tT_i, M_i ] = SLAMICP( M_i-1, T_i, 0, method, 0, P_i, 0 );

% Obtain tT_i (transformed T_i using P_i )
>> [ ~, ~, ~, ~, ~, tT_i ] = SLAMICP( M, T_i, 0, method, 0, P_i );

05-12-2023: SLAMICP_V51.rar - Includes a precompiled MEX file for MATLAB under Windows®

The SLAMICP function computes the transformation (P_i) that aligns the input point cloud (T_i) with a reference point cloud (M).
A MATLAB wrapper is provided as precompiled MEX file for Windows®.

% Call to match T_i with M_i-1
>> [ P_i, niter, md, O_indx, O_coords, tT_i, M_i ] = SLAMICP( M_i-1, T_i, inlier_threshold, method, maxiter, P_i-1, Outlier_threshold );   % slower, ideal for SLAM (create M_i )
>> [ P_i, niter, md, O_indx, O_coords, tT_i ] = SLAMICP( M, T_i, inlier_threshold, method, maxiter, P_i-1, Outlier_threshold );
>> [ P_i, niter, md, O_indx, O_coords ] = SLAMICP( M, T_i, inlier_threshold, method, maxiter, P_i-1, Outlier_threshold );
>> [ P_i, niter, md ] = SLAMICP( M, T_i, inlier_threshold, method, maxiter, P_i-1, Outlier_threshold );
>> [ P_i, niter] = SLAMICP( M, T_i, inlier_threshold, method, maxiter, P_i-1, Outlier_threshold );   % faster
>> [ P_i ] = SLAMICP( M, T_i, inlier_threshold, method, maxiter, P_i-1, Outlier_threshold );      % ideal for mobile robot self-localization, P_i = ( x_i, y_i, θ_i )
>> [ P_i ] = SLAMICP( M, T_i, inlier_threshold, method, maxiter, P_i-1 );      % Outlier_threshold = inlier_threshold

% Display the help and usage instructions
>> SLAMICP( );

% Obtain the outliers of tT_i (transformed T_i according to P_i ), matching and merging only the outliers of tT_i (listed in O_coords ) with M_i-1 (no ICP iterations) to create M_i
>> [ ~, ~, ~, O_index, O_coords, tT_i, M_i ] = SLAMICP( M_i-1, T_i, inlier_threshold, method, 0, P_i, Outlier_threshold );

% Obtain the outliers of tT_i (transformed T_i according to P_i )
>> [ ~, ~, ~, O_index, O_coords, tT_i] = SLAMICP( M, T_i, inlier_threshold, method, 0, P_i, Outlier_threshold );

% Obtain tT_i (transformed T_i according to P_i ) and merge all points of tT_i (all are outliers because Outlier_threshold = 0 ) with M_i-1 (no ICP iterations) to create M_i
>> [ ~, ~, ~, O_index, O_coords, tT_i, M_i ] = SLAMICP( M_i-1, T_i, 0, method, 0, P_i, 0 );

% Obtain tT_i (transformed T_i using P_i )
>> [ ~, ~, ~, ~, ~, tT_i ] = SLAMICP( M, T_i, 0, method, 0, P_i );

16-05-2023: SLAMICP_V41.rar - First version published online ( includes a precompiled MEX file for MATLAB under Windows® )

The PCMerge function applies a transformation to the current LIDAR scan (T_i) and merges the result with the reference point cloud (M_i-1).
A MATLAB wrapper is provided as precompiled MEX file for Windows®.

% Create an updated map M_i : 1) transform T_i using P_i = ( x_i, y_i, θ_i ) obtained with SLAMICP and 2) merge the result with the original map M
>> M_i = PCMerge( M_i-1, T_i, P_i );

% Create an updated map M_i : 1) transform T_i using Tr_fit = ( R( θ ), t ) obtained with LIBICP and 2) merge the result with the original map M
>> M_i = PCMerge( M_i-1, T_i, Tr_fit );

16-05-2023: PCMerge_MEX_V11.rar - First version published online ( includes a precompiled MEX file for MATLAB under Windows® )

The ComputeNormals function computes the normals of a point cloud.
A MATLAB wrapper is provided as precompiled MEX file for Windows®.

% Optimized computation of the normals N (red arrows) of a map M (blue dots)
>> N = CalculateNormals(M);

29-05-2023: ComputeNormals_V1.rar - First version published online ( includes a precompiled MEX file for MATLAB under Windows® )

Boost libraries - Used by the k-d tree search

CMake - Requiered to control the software compilation

The code of the SLAMICP library is published under the GNU General Public License.

		Direct download of the video (elevator.mp4, 560MB)

Eduard Clotet & Jordi Palacín

Main paper featuring the SLAMICP Library (please add citation if you use the library):

SLAMICP Library: Accelerating Obstacle Detection in Mobile Robot Navigation via Outlier Monitoring following ICP Localization, Sensors 2023, 23, 6841.

Other related papers:

Path Planning of a Mobile Delivery Robot Operating in a Multi-Story Building Based on a Predefined Navigation Tree, Sensors 2023, 23, 8795.

A Procedure for Taking a Remotely Controlled Elevator with an Autonomous Mobile Robot Based on 2D LIDAR, Sensors 2023, 23, 6089.